Formale Systeme

EINER DER Zentralbegriffe in diesem Buch ist der des formalen Systems. Die Art von formalen Systemen, die ich verwende, hat der amerikanische Logiker Emil Post in den Zwanzigerjahren er-funden. Sie wird oft als "Postsches Produktionssystem" bezeichnet. Dieses Kapitel führt dem Leser ein formales System vor, und darüber hinaus hoffe ich, dass er dieses formale System zumindest ein bisschen zu erforschen wünscht; um seine Neugier zu reizen, habe ich ein kleines Rätsel ent-worfen.

Es lautet: "Können Sie MU erzeugen?" Zunächst werde ich Ihnen eine Kette vor-
legen, d. h. eine Kette von Zeichen*. Damit Sie nicht gleich ungeduldig werden: diese Kette ist MI. Dann geben wir Ihnen einige Regeln, mit denen Sie eine Kette in eine andere verwandeln können. Wenn zu einem gewissen Zeitpunkt eine dieser Regeln anwendbar ist und Sie sie verwenden möchten, können Sie das tun - aber es gibt keine Vorschrift, welche Regel Sie verwenden sollen, wenn mehrere anwendbar sind. Das können Sie entscheiden - und das ist natürlich der Punkt, an dem das Spielen mit dem formalen System so etwas wie eine Kunst werden kann. Die Hauptsache, die fast nicht erwähnt zu werden braucht, ist, dass Sie nichts tun dürfen, was die Regeln verletzt. Wir können diese Einschränkung die "Formalitätsbedingung" nennen. In diesem Kapitel bedarf das wahrscheinlich keiner Betonung. So seltsam es aber klingen mag - ich sage Ihnen voraus, dass Sie, wenn Sie mit einigen formalen Systemen in späteren Kapiteln spielen, feststellen werden, dass Sie die Formalitätsbedingung immer und immer wieder verletzen werden, wenn Sie nicht bereits früher mit formalen Systemen gearbeitet haben.

Bei unserem formalen System - dem MIU-System - ist als erstes zu sagen, dass es nur drei Buchstaben des Alphabets verwendet, nämlich M, I und U. Das bedeutet, dass die einzigen Ketten des MIU-Systems diejenigen sind, die sich aus diesen drei Buchstaben zusammensetzen. Nachstehend einige Ketten des MIU-Systems:

MU
UIM
MUUMUU
UIIUMIUUIMUIIUMIUUIMUIIU

* In diesem Buch halten wir uns an folgende Konventionen, wenn wir von Zeichenketten reden: wenn die Zeichenkette in der gleichen Schriftart ist wie der Text, wird sie in einfachen oder doppelten Anführungszeichen eingeschlossen. Interpunktionen, die zum Satz und nicht zur Kette gehören, stehen logischerweise außerhalb der Anführungszeichen. Z. B. ist der erste Buchstabe dieses Satzes "Z", während der erste Buchstabe von "diesem Satz" "d" ist. Wenn die Kette in der Schriftart Syntax gesetzt ist, lassen wir die Anführungszeichen im allgemeinen weg, wenn sie nicht um der Klarheit willen nötig sind. Der erste Buchstabe von Syntax ist
z. B. S.

Obgleich jedoch all das legitime Ketten sind, sind es nicht Ketten, die Sie "besitzen". Die einzige Kette in Ihrem Besitz ist vorderhand MI. Nur wenn Sie die Regeln anwenden, die wir gleich ange-ben werden, können Sie Ihre private Sammlung erweitern.
Hier die erste Regel:

REGEL I: Wenn Sie eine Kette besitzen, deren letzter Buchstabe I ist, können Sie am Schluss ein U zufügen.

Wenn Sie es übrigens noch nicht erraten haben sollten, eine der Bedeutungen von
"Kette" ist die, dass die Buchstaben in einer feststehenden Ordnung sind. Zum Beispiel sind MI und IM zwei verschiedene Ketten. Eine Kette von Symbolen ist nicht einfach ein "Sack" voller Symbole, bei dem die Ordnung keine Rolle spielt.
Hier die zweite Regel:

REGEL II: Angenommen Sie haben Mx Dann können Sie Ihrer Sammlung Mxx zufügen.

Was ich damit meine, zeigen die folgenden Beispiele:

Aus MIU können Sie MIUIU erhalten.
Aus MUM können Sie MUMUM erhalten.
Aus MU können Sie MUU erhalten.

So steht also der Buchstabe "x" in der Regel für irgendeine Kette; wenn Sie aber einmal entschieden haben, für welche, müssen Sie bei Ihrer Entscheidung bleiben (bis Sie die Regel wieder anwenden. An diesem Punkt können Sie eine neue Wahl treffen). Beachten Sie das dritte Beispiel. Es zeigt, wie Sie, wenn Sie MU besitzen, eine weitere Kette in Ihre Sammlung aufnehmen können - aber zuerst müssen Sie MU haben! Zu dem Buchstaben "x" noch ein letzter Kommentar: Er gehört dem formalen System nicht in der gleichen Art und Weise an wie die drei Buchstaben "M", "I" und "U". Indessen ist es nützlich, eine Möglichkeit zu haben, allgemein, symbolisch über die Ketten des Systems sprechen zu können, und das ist die Funktion von "x": eine beliebige Kette zu repräsentieren. Wenn Sie jemals eine Kette, die ein "x" enthält, Ihrer "Sammlung" einverleiben, haben Sie etwas falsch gemacht, denn Ketten des MIU-Systems enthalten niemals "x"!
Die dritte Regel:

REGEL III: Wenn in einer der Ketten Ihrer Sammlung III vorkommt, können Sie eine neue Kette mit U anstelle von III bilden.

Beispiele:

Aus UMIIIMU können Sie UMUMU machen.
Aus MIIII können Sie MIU (oder auch MUI) machen.
Bei IIMII kommen Sie mit dieser Regel nicht weiter.
(Die drei I müssen aufeinander folgen.)
Aus MIII ergibt sich MU.

Unter keinen Umständen dürfen Sie annehmen, dass Sie diese Regel auch rückläufig verwenden können wie im folgenden Beispiel:
Aus MU mache MIII. <= Das ist falsch.
Regeln sind Einbahnstraßen. Hier die letzte Regel:

REGEL IV: Wenn UU in einer Ihrer Ketten vorkommt, kann man es streichen.
Aus UUU ergibt sich U.
Aus MUUUIII ergibt sich MUIII.

Das wär's. Nun können Sie beginnen, zu versuchen, MU zu erzeugen. Es macht nichts, wenn es Ihnen nicht gelingt. Versuchen Sie es ein bisschen - die Hauptsache ist, dass Sie auf den Geschmack dieses MU-Rätsels kommen. Viel Vergnügen.

Sätze, Axiome, Regeln

Die Lösung des MU-Rätsels geben wir später in diesem Buch. Wichtig ist im Augenblick nicht die Lösung, sondern die Suche nach ihr. Sie haben wahrscheinlich ein paar Versuche gemacht, MU zu erzeugen. Dabei haben Sie Ihre eigene Sammlung von Ketten aufgebaut. Solche durch die Regeln herstellbare Ketten nennt man SÄTZE. Der Ausdruck "Satz" hat natürlich im mathematischen Sprachgebrauch eine Bedeutung, die ganz anders ist als die unsrige. Er bedeutet eine Aussage in gewöhnlicher Sprache, die durch rigorose Beweisführung als wahr erkannt worden ist, wie Zenos Satz [Vgl. Protokoll Seite 1]von der "Unexistenz" der Bewegung oder Euklids Satz von der Unend-lichkeit der Primzahlen. In einem formalen System aber braucht man SÄTZE nicht als Aussagen zu betrachten - sie sind lediglich Symbolketten. Und sie werden nicht bewiesen, sondern einfach wie
von einer Maschine nach gewissen typographischen Regeln erzeugt. Um diese wichtige Unter-scheidung in der Bedeutung des Wortes "Satz" zu betonen, gehe ich in diesem Buch wie folgt vor: wenn "Satz" in normalen Buchstaben wiedergegeben wird, hat das Wort seine alltägliche Bedeutung - ein Satz ist eine Aussage in der gewöhnlichen Sprache, die jemand einmal durch logische Argumenta-tion als wahr bewiesen hat. Wenn in Großbuchstaben, soll "SATZ" seine technische Bedeutung ha-ben: eine in einem formalen System erzeugbare Kette. Das MU-Puzzle stellt die Frage, ob MU ein SATZ des MIU-Systems ist.

Ich gab Ihnen einen SATZ zu Beginn vor, nämlich MI. Ein solcher SATZ, den man "umsonst" erhält, heißt Axiom - und wiederum ist die technische Bedeutung von der gängigen völlig verschieden. Ein formales System kann kein, ein, mehrere, ja sogar unendlich viele Axiome besitzen. Beispiele für alle diese Typen werden wir in diesem Buch finden.

Jedes formale System hat Regeln für das Rangieren von Symbolen wie etwa die vier Regeln des MIU-Systems. Diese Regeln nennt man entweder Erzeugungs-Regeln oder Schluss-Regeln. Ich werde beide Ausdrücke benützen.

Der letzte Begriff, den ich hier einführen will, ist der der Ableitung. Ich gebe hier eine Ableitung des SATZES MUIIU:

1) MI ......... Axiom
2) MII ....... aus 1) durch Regel II
3) MIIII ..... aus 2) durch Regel II
4) MIIIIU ... aus 3) durch Regel I
5) MUIU ......aus 4) durch Regel III
6) MUIUUIU .aus 5) durch Regel II
7) MUIIU .... aus 6) durch Regel IV

Einen SATZ abzuleiten bedeutet, explizit schrittweise zu zeigen, wie man den SATZ nach den Regeln des formalen Systems erzeugen kann. Der Begriff der Ableitung ist dem des Beweises nachgebildet, aber eine Ableitung ist eine strengere Verwandte des Beweises. Es würde seltsam klingen, zu sagen, dass man MUIIU bewiesen hat, aber es klingt weniger seltsam, zu sagen, dass man MUIIU abgeleitet hat.

Innerhalb und außerhalb des Systems

Die meisten Leute gehen das MU-Rätsel an, indem sie eine Anzahl von SÄTZEN ableiten, ganz nach Belieben, einfach um zu sehen, was dabei herauskommt. Sehr bald beginnen sie, gewisse Eigen-schaften der von Ihnen gefundenen SÄTZE zu erkennen; hier betritt die menschliche Intelligenz die Bildfläche. Zum Beispiel lag es wohl nicht auf der Hand, dass alle SÄTZE mit M beginnen, bis man einige ausprobiert hatte. Dann trat das Muster zutage, und man konnte es nicht nur erkennen, sondern auch verstehen, wenn man einen Blick auf die Regeln warf, die bewirken, dass jeder neue SATZ seinen Anfangsbuchstaben von einem früheren SATZ erbt; schließlich können dann die An-fangsbuchstaben aller Sätze bis zum ersten Buchstaben des einzigen Axioms MI zurückverfolgt werden, und das ist ein Beweis dafür, dass alle Sätze des
MIU-Systems mit M beginnen müssen.

Was hier geschieht ist höchst bedeutsam. Es zeigt einen Unterschied zwischen Mensch und Maschine. Es wäre sicher möglich - es wäre sogar sehr leicht - einen Computer so zu programmieren, dass er einen SATZ des MIU-Systems nach dem ändern erzeugt, und wir könnten ins Programm den Befehl einbauen, erst dann aufzuhören, wenn U erzeugt worden ist. Jetzt wissen Sie, dass ein so programmierter Computer nie anhalten würde. Und das erstaunt Sie weiter nicht. Was aber, wenn Sie einen Freund bitten würden, zu versuchen, U zu erzeugen? Sie wären nicht überrascht, wenn er nach einer Weile zurückkäme und sich beklagte, dass er das M am Anfang nicht loswerden könne und dass es deshalb vergebliche Mühe sei. Auch wenn einer nicht besonders hell ist, wird er über das, was er tut, gewisse Beobachtungen anstellen, und diese Beobachtungen geben ihm einen guten Einblick in die Aufgabe - einen Einblick, der dem Computer-Programm, wie wir es beschrieben haben, abgeht.

Nun will ich aber sehr genau ausführen, was ich andeutete, als ich sagte, hier zeige sich ein Unter-schied zwischen Mensch und Maschine. Ich meinte damit, dass es möglich ist, eine Maschine zur Lösung einer Routine-Aufgabe so zu programmieren, dass die Maschine selbst die offensichtlichsten Tatsachen über ihre Tätigkeit niemals wahrnimmt; zum menschlichen Bewusstsein jedoch gehört es, gewisse Tatsachen dessen, was man tut, wahrzunehmen. Aber das haben Sie schon immer ge-wusst. Wenn Sie auf einer Additionsmaschine " 1" tippen, dann 1 addieren und dann nochmals 1 addieren usw. usf. und das Stunden und Stunden lang, wird die Maschine nie lernen, Ihnen zuvor-zukommen und es selbst zu tun. Und doch würde jeder Mensch dieses Wiederholungsverhalten sehr rasch aufgreifen. Oder, um ein etwas albernes Beispiel zu nehmen: ein Auto wird, so viel und so gut es auch gefahren wurde, niemals auf den Gedanken kommen, dass es andere Autos und Hindernisse auf der Straße meiden sollte, und es wird auch niemals die von seinem Eigentümer am häufigsten befahrene Route erlernen.

Der Unterschied ist somit, dass es für eine Maschine möglich ist, unaufmerksam zu
sein; für einen Menschen ist es unmöglich. Man beachte, dass ich nicht sage, alle
Maschinen seien notwendigerweise unfähig, differenzierte Beobachtungen anzustellen: Ich sage nur, dass gewisse Maschinen es sind. Ich sage auch nicht, dass alle
Menschen immer differenzierte Beobachtungen machen; Menschen sind in Wirklichkeit oft sehr un-aufmerksam. Man kann aber Maschinen völlig unaufmerksam machen, Menschen jedoch nicht. Tat-sächlich sind bis heute die meisten bisher gebauten Maschinen fast gänzlich unaufmerksam. Das ist wahrscheinlich der Grund, warum die Eigenschaft, unaufmerksam zu sein, für die meisten Leute das Charakteristikum der Maschine zu sein scheint. Wenn zum Beispiel jemand sagt, eine Aufgabe sei "mechanisch", dann heißt das nicht, dass die Menschen unfähig sind, diese Aufgabe zu lösen; es heißt jedoch, dass nur eine Maschine es ohne Klage und ohne Langeweile immer und immer wieder tun könnte.

Aus dem System hinausspringen

Es ist eine der Intelligenz inhärente Eigenschaft, dass sie aus einer Tätigkeit, der sie sich widmet, hinausspringen und beurteilen kann, was sie getan hat - sie sucht immer und findet oft Muster. Nun sagte ich zwar, dass eine Intelligenz aus ihrer Tätigkeit hinausspringen kann, aber das bedeu-tet nicht, dass sie es immer tut. Doch wird ein bisschen Nachhilfe oft genügen. Z. B. könnte ein Mensch, der ein Buch liest, schläfrig werden. Anstatt weiterzulesen, bis er mit dem Buch zu Ende ist, wird er es wahrscheinlich weglegen und das Licht ausschalten. Er ist "aus dem System" he-rausgetreten, und das scheint uns die natürlichste Sache der Welt zu sein. Oder nehmen wir an, dass A Fernsehen schaut und B ins Zimmer kommt und Zeichen offensichtlichen Unmuts über die Situation bekundet. A denkt vielleicht, dass er das Problem verstehe, und versucht die Schwierig-keit zu beheben, indem er das gegenwärtige System (das Fernsehprogramm) verlässt und die Ka-näle durchprobiert, um ein besseres Programm zu erwischen. B hat vielleicht eine radikalere Vor-stellung davon, was es bedeutet, das "System zu verlassen" - nämlich den Fernseher abzuschalten. Natürlich gibt es Fälle, in denen nur wenige Personen den nötigen Überblick haben, um ein System zu erkennen, das das Leben vieler Menschen beherrscht, ein System, das nie zuvor überhaupt als System erkannt worden war; dann bringen diese Leute oft ihr ganzes Leben damit zu, andere Leute davon zu überzeugen, dass das System wirklich vorhanden ist und dass man es verlassen solle!

Wie gut hat man die Computer gelehrt, aus dem System hinauszuspringen? Ich erwähne ein Beispiel, das manche Beobachter überraschte. Vor kurzem hatte bei einem Computer-Schachturnier in Kanada ein Programm - das schwächste von allen - die ungewöhnliche Eigen-schaft aufzugeben, lange bevor die Partie zu Ende war. Es spielte nicht sehr gut, aber es hatte wenigstens den Vorzug, dass es eine hoffnungslose Stellung erkennen und sofort aufgeben konnte, anstatt zu warten, bis die anderen Programme das langweilige Ritual der Mattsetzung hinter sich gebracht hatten. Auch wenn es jede Partie, die es spielte, verlor, tat es das stilvoll. Viele der anwesenden Schachexperten waren beeindruckt. Wenn man also das "System" definiert als "in einer Schachpartie Züge machen", ist es klar, dass dieses Programm eine raffinierte vorprogrammierte Fähigkeit besaß, das System zu verlassen. Wenn man anderseits das "System" als das auffasst, "was der Computer zu tun programmiert wurde", dann besteht kein Zweifel, dass der Computer überhaupt keinerlei Fähigkeit besaß, das System zu verlassen.

Beim Studium formaler Systeme ist die Unterscheidung zwischen der Arbeit innerhalb des Systems und den Aussagen und Beobachtungen über das System äußerst wichtig. Ich nehme an, dass Sie mit dem MU-Puzzle wie die meisten Leute begannen, indem Sie innerhalb des Systems arbeiteten, dass Sie dann allmählich besorgt wurden, und diese Sorge steigerte sich bis zu dem Punkt, wo Sie ohne die Notwendigkeit weiterer Überlegung aus dem System heraustraten und versuchten, sich klar zu werden, warum Ihnen nicht gelungen war, MU zu erzeugen. Vielleicht fanden Sie einen Grund, warum Sie das nicht konnten; das hieße Nachdenken über das System. Vielleicht erzeugten Sie irgendwann einmal MIU, das hieße innerhalb des Systems arbeiten. Nun soll das aber nicht bedeuten, dass diese beiden Betrachtungsweisen miteinander völlig unverträglich sind; ich bin sicher, dass jeder Mensch bis zu einem gewissen Grad fähig ist, inner-halb eines Systems zu arbeiten und gleichzeitig über das nachzudenken, was er tut. In Angelegenheiten, die den Menschen betreffen, ist es häufig so gut wie unmöglich, die Dinge säuberlich in "innerhalb des Systems" und "außerhalb des Systems" aufzuteilen; das Leben setzt sich aus so vielen ineinandergreifenden und miteinander verwobenen und oft widerspruchsvollen Systemen zusam-men, dass es allzu einfach scheinen mag, die Dinge unter diesem Aspekt zu betrachten. Indes ist es oft wichtig, einfache Vorstellungen sehr klar zu definieren, damit man sie beim Nachdenken über komplizierte Vorstellungen als Modelle benutzen kann. Und das ist der Grund, warum ich Ihnen formale Systeme vorführe; und es ist an der Zeit, dass wir zu unserer Diskussion des MIU-Systems zurückkehren.

M-Modus, I-Modus, U-Modus

Das MU-Rätsel war so formuliert, dass es zu einer Forschertätigkeit innerhalb des MIU-Systems Anstoß gab. Es war aber auch so formuliert, dass es nicht zu der Ansicht verführen sollte, das Verbleiben innerhalb des Systems bringe notwendigerweise Früchte. Deshalb führte es zu einem gewissen Schwanken zwischen den beiden Arbeitsweisen. Eine Methode zur Trennung dieser beiden Modi wäre die, zwei Blätter zu nehmen. Auf dem einen arbeiten Sie "in Ihrer Eigenschaft als Maschine", werden also das Blatt mit nichts als M's, I's und U's füllen; auf dem zweiten Blatt arbeiten Sie in Ihrer Eigenschaft als "denkendes Wesen", und es steht Ihnen frei, zu tun was immer Ihre Intelligenz vorschlägt - den Gebrauch der deutschen Sprache, das Skizzieren von Ideen, das Ar-beiten von hinten nach vorn, dann den Gebrauch von Kurzschrift (wie etwa des Buchstabens "x"), die Zusammenziehung verschiedener Schritte zu einem einzigen, die Änderung der Systemregeln, um zu sehen, was dabei herauskommt, oder was immer sonst Ihnen einfällt. Etwas, was Ihnen vielleicht auffällt, ist dass die Zahlen 3 und 2 eine wichtige Rolle spielen, da die I's in Dreiergrup-pen ausgemerzt werden, die U's in Paaren, und die Verdoppelung der Länge (ausgenommen M) durch Regel II erlaubt wird. So könnte auch das zweite Blatt ein paar Berechnungen enthalten. Wir werden gelegentlich auf diese zwei Arten, sich mit dem formalen System auseinanderzusetzen, zurückkommen, und wir nennen sie Mechanischen Modus (M-Modus) und Intelligenz-Modus (I-Modus). Um unsere Modi zu vervollständigen, so dass jeder einem Buchstaben des MIU-Systems entspricht, sei noch der letzte genannt: der Un-Modus (U-Modus), die Art und Weise, wie Zen sich mit den Dingen auseinandersetzt. Mehr darüber in späteren Kapiteln.

Entscheidungsverfahren

Etwas, das sich an diesem Rätsel beobachten lässt, ist, dass es Regeln mit zwei gegensätzlichen Tendenzen verwendet, die Verlängerungsregeln und die Verkürzungsregeln. Zwei Regeln (I und II) gestatten, die Kette zu verlängern (aber natürlich nur auf die vorgeschriebene sehr starre Art und Weise); und die zwei anderen, die Kette etwas schrumpfen zu lassen (wieder auf sehr eingeschränkte Art). Für die Reihenfolge, in der die Regeln angewendet werden können, gibt es anscheinend endlose Möglichkeiten, und das nährt die Hoffnung, dass MU irgendwie erzeugt werden könne. Vielleicht führt es dazu, die Kette bis zu einer gigantischen Länge auszudehnen, und dann ein Stück nach dem ändern herauszunehmen, bis nur noch zwei Symbole übrigbleiben, oder, schlimmer noch, es könnte aufeinanderfolgende Phasen von Ausdehnung und dann wieder Schrumpfung und dann wieder Ausdehnung und Schrumpfung usw. mit sich bringen. Aber eine Garantie gibt es nicht. Tatsächlich haben wir ja bereits festgestellt, dass U überhaupt nicht herstellbar ist und es keinerlei Unterschied macht, wenn man bis in alle Ewigkeit verlängert und verkürzt.

Doch scheinen der Fall U und der Fall MU ganz verschieden zu sein. Denn wir erkennen die Un-möglichkeit, U herzustellen, an einer sehr oberflächlichen Eigenschaft: Es beginnt nicht mit M, und das müssen doch alle SÄTZE tun. Eine solch einfache Methode, Nicht-SÄTZE zu entdecken, ist sehr bequem. Wer jedoch sagt uns, dass dieser Test alle Nicht-SÄTZE aufdeckt? Es muss doch eine große Anzahl von SÄTZEN geben, die mit M beginnen, die aber nicht erzeugbar sind. Vielleicht ist MU einer davon. Das würde bedeuten, dass der "Anfangsbuchstaben-Test" von beschränkter Brauchbarkeit ist. Er deckt nur einen Teil der Nicht-SÄTZE auf, erfasst andere aber nicht. Indessen verbleibt die Möglichkeit eines noch komplizierteren Tests, der zwischen den Ketten, die durch die Regeln hergestellt werden können, und denen, die es nicht tun, genau unterscheidet. Hier sehen wir uns vor der Frage: "Was meinen wir mit Test?" Es ist vielleicht nicht klar, warum eine solche Frage in diesem Zusammenhang sinnvoll oder wichtig ist. Ich will jedoch ein Beispiel eines "Tests" geben, das dem Sinn des Wortes Gewalt anzutun scheint.

Stellen Sie sich einen Dämon vor, der unendlich viel Zeit hat, und dem es Spaß macht, Sätze des MIU-Systems zu produzieren, und das auf einigermaßen methodische Weise. Der Dämon könnte zum Beispiel so vorgehen:

Schritt 1: Wende jede anwendbare Regel auf das Axiom MI an. Das ergibt zwei neue SÄTZE: MIU, MII.
Schritt 2: Wende jede anwendbare Regel auf die in Schritt 1 erzeugten SÄTZE an.
Das ergibt drei neue SÄTZE: MIIU, MIUIU, MIIII.
Schritt 3: Wende jede anwendbare Regel auf die in Schritt 2 erzeugten SÄTZE an.
Das ergibt fünf neue SÄTZE: MIIIIU, MIIUIIU, MIUIUIUIU, MIIIIIIII, MUI.
.
.
.

Früher oder später erzeugt dieses Vorgehen jeden einzelnen SATZ, weil die Regeln in jeder mögli-chen Reihenfolge angewendet wurden (siehe Abb. 11). Irgendwann einmal werden alle die er-wähnten Verlängerungen und Verkürzungen ausgeführt sein. Indessen ist nicht klar, wie lange man darauf warten muss, bis eine bestimmte Kette in dieser

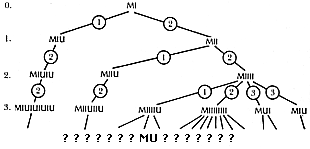
Abb. 11. Ein systematisch konstruierter "Baum" aller SÄTZE des MW-Systems. Die N-te Stufe von oben enthält jene SÄTZE, deren Ableitungen genau N Schritte umfassen. Die Ziffern in den Ringen geben an, welche Regeln angewendet wurden. Ist MU irgendwo in diesem Baum?

Liste erscheint, da die SÄTZE gemäß der Kürze ihrer Ableitung aufgeführt werden. Wenn man an einer besonderen Kette, wie z. B. MU interessiert ist, und nicht einmal weiß, ob sie überhaupt abgeleitet werden kann, und noch viel weniger, wie lang diese Ableitung sein könnte, ist das keine sehr brauchbare Anordnung.
Wir geben nunmehr den "SATZheit-Test":

Warten Sie, bis die fragliche Kette hergestellt ist; wenn das geschieht, wissen Sie, dass sie ein SATZ ist - und wenn es nie geschieht, wissen Sie, dass sie kein SATZ ist.

Auf den ersten Blick ist das lächerlich, denn es setzt voraus, dass wir bereit sind, buchstäblich unendlich lange auf unsere Antwort zu warten. Das bringt uns zum Kern der Frage, was als "Test" gelten soll. Von entscheidender Wichtigkeit ist eine Garantie, dass wir unsere Antwort in einem endlichen Zeitabschnitt erhalten. Wenn es einen Test für SATZheit gibt, einen Test, der immer in einer endlichen Zeitspanne ein Ende findet, dann nennt man diesen Test ein Entscheidungs-verfahren für das vorliegende formale System.

Wenn Sie über ein Entscheidungsverfahren verfügen, dann haben Sie eine sehr konkrete Charakterisierung aller SÄTZE in dem System. Auf den ersten Blick könnte man vielleicht meinen, dass die Regeln und Axiome des formalen Systems eine nicht weniger vollständige Cha-rakterisierung der SÄTZE des Systems liefern als ein Entscheidungsverfahren. Das heikle Wort ist hier "Charakterisierung". Gewiss charakterisieren die Schlussregeln und Axiome des MIU-Systems implizit diejenigen Ketten, die SÄTZE sind. Sogar noch impliziter charakterisieren sie die Ketten, die nicht SÄTZE sind. Aber implizite Charakterisierung genügt für viele Zwecke nicht. Wenn jemand behauptet, dass er eine Charakterisierung aller SÄTZE besitze, aber unendlich viel Zeit zu dem Schluss braucht, dass eine gewisse Kette kein SATZ ist, wäre man wohl geneigt zu sagen, dass et-was an dieser Charakterisierung fehlt. Sie ist nicht konkret genug. Und aus diesem Grunde ist es ein sehr wichtiger Schritt, herauszufinden, ob es ein Entscheidungsverfahren gibt. Was diese Ent-deckung tatsächlich bedeutet, ist, dass man einen Test darüber durchführen kann, ob eine Kette einen SATZ darstellt und dass der Test, auch wenn er kompliziert ist, garantiert ein Ende findet. Prinzipiell ist der Test genauso leicht, genauso mechanisch, genauso finit, genauso sicher, wie die Prüfung, ob der erste Buchstabe der Kette M ist. Ein Entscheidungsverfahren ist ein "Lackmus-Test" für SÄTZE.

Übrigens ist es eine Bedingung für formale Systeme, dass das Bündel von Axiomen durch ein Entscheidungsverfahren gekennzeichnet ist - es muss einen Lackmus-Test für Axiomheit geben. Das gewährleistet, dass man zumindest am Anfang ohne weiteres in Gang kommen kann. Das ist der Unterschied zwischen der Menge der Axiome und der Menge der SÄTZE; die erste hat immer ein Entscheidungsverfahren, die letzte braucht keines zu haben.

Sie werden sicher zugeben, dass Sie sich beim ersten Blick auf das MIU-System genau diesem Problem gegenübersahen. Das einzige Axiom war bekannt, die Schluss-Regeln waren einfach, so waren die SÄTZE also implizit charakterisiert - und doch war es noch immer ganz unklar, was die Konsequenzen dieser Charakterisierung waren. Insbesondere war noch völlig unklar, ob MU ein SATZ ist oder nicht.